Vor vielen Jahren bin ich bei den Dreharbeiten zu meinem Dokumentarfilm "Doktor Jennys Klangfiguren" auf die unzähligen harmonischen Muster und Strukturen aufmerksam geworden, die sich bei den Lebewesen in der Natur finden. Der Biologe Ernst Haeckel hat sie "Kunstformen der Natur" genannt, und der Bildhauer Karl Blossfeld sprach von "Urformen der Kunst". Im Laufe der Jahre habe ich hunderte von Fotos gemacht, um diese "Wunder der Schönheit" zu dokumentieren. Ich möchte davon eines Tages eine größere Ausstellung machen, derzeit fehlen mir dafür noch die Mittel. Im Folgenden möchte ich einige Beispiele dafür vorstellen.
Kunstformen der Natur - Urformen der Kunst
Auf den ersten Blick erscheint die Fülle und Vielfalt der Naturformen eher verwirrend. Bei näherer Betrachtung aber lässt sich ein gemeinsames ästhetisches Grundprinzip erahnen, das Goethe meinte, als er schrieb: “Alle Gestalten sind ähnlich - doch keine gleichet der anderen. Und so deutet das Chor auf ein geheimes Gesetz, auf ein heiliges Rätsel...”
Die Basis der Ordnung: Radiale Symmetrien
Was bei den meisten Pflanzen und einfachen Tieren als erstes ins Auge fällt, sind die radialsymmetrischen Formen. Sie haben mehrere Symmetrieachsen, die vom Mittelpunkt nach außen streben: Kreis und Kugel, Dreieck-Sechseck-Zwölfeck-, Viereck-Achteck- und Fünfeck-Zehneck-Symmetrien.
An der Fünfzahl orientieren sich alle Rosengewächse. Auf der Hagebutte erkennt man, wenn die Blütenblätter abgefallen sind, ein klares Pentagon, die Kelchblätter bilden ein Pentagramm.
Die Apfelblüte zeigt fünf Blütenblätter, und im horizontal halbierten Apfel findet sich das Pentagramm im Kerngehäuse wieder.
Es sind vor allem die zweikeimblättrigen Pflanzen, die Fünfeck- und, weniger häufig, auch Vierecksymmetrien zeigen.
Die Einkeimblättrigen hingegen bevorzugen ganz offensichtlich die Dreieck-Sechseck-Symmetrie, besonders deutlich zu erkennen bei den Tulpen und Lilien.
Warum ist das so? Eine Frage, auf die man zur Zeit von den Biologen noch keine befriedigende Antwort bekommt.
Natürlich finden sich diese harmonischen, radialsymmetrischen Formen nicht nur bei Pflanzen.
Vor allem auch bei vielen Meerestieren, bei Seesternen beispielsweise, Quallen und Radiolarien - winzig kleinen, einzelligen Meerestieren - sind die Vier- Fünf- und Sechsecksymmetrien in unzähligen Variationen vertreten. Diese radialsymmetrischen Formen finden sich interessanterweise auch in den Klangfiguren des Schweizer Arztes Dr. Hans Jenny, bei denen verschiedene Substanzen (Sand, Wasser, u.a.) in Schwingung versetzt wurden. Genaueres darüber weiter unten.
Ein universelles Gestaltungsprinzip: der “Goldene Schnitt”
Bei Betrachtung der Proportionen in den Gestalten von Pflanzen und Tieren begegnen wir immer wieder Zahlen aus einer mathematischen Reihe, die nach ihrem Entdecker Leonardo Fibonacci, “Fibonaccireihe” genannt wird.
Diese Reihe entsteht dadurch, dass man zu einer Zahl die ihr jeweils vorausgehende Zahl addiert. Begonnen wird mit 1. Davor liegt Null, also: 0 und 1 gibt 1. 1 und 1 gibt 2, 2 und 1 gibt 3, 3 und 2 gibt 5, 5 und 3 gibt 8 - etcetera: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, ... und immer so weiter, ad infinitum.
Das Verhältnis zweier benachbarter Zahlen dieser Reihe entspricht - um so genauer, je größer die Zahlen sind - der Zahl Phi: 1,61803398874989... (usw.) Diese Zahl beschreibt auch das Verhältnis der beiden Seiten einer im “Goldenen Schnitt” geteilten Strecke.
Das Prinzip des “Goldenen Schnittes” besteht darin, eine Strecke so zu teilen, dass der größere Teil zum Ganzen im gleichen Verhältnis steht, wie der kleinere Teil zum Größeren.
Dieses harmonische und ganzheitliche Teilungsverhältnis findet sich in der gesamten belebten Natur wieder, quer durch alle Reiche, Klassen und Arten von Lebewesen, vom mikroskopisch kleinen Einzeller, einer Radiolarie zum Beispiel, bis zu den größten Lebewesen, die jemals existiert haben. Es findet sich in den Knochen eines Dinosaurierskeletts ebenso, wie in den Knochen einer menschlichen Hand, in Blättern und Blumen,
in Fischen und Vögeln, im Körperbau von Käfern und in den Flügelproportionen von vielen Schmetterlingen.
Es ist eine uralte und universelle Formensprache, auf die sich - wie und warum auch immer - alle Lebewesen (oder jedenfalls die überwiegende Mehrheit) schon vor vielen hundert Jahrmillionen geeinigt zu haben scheinen.
Die unendliche Spirale
Die Fibonacci-Reihe liegt auch der logarithmischen Spirale zu Grunde, einem weiteren Grundmuster in den Bauplänen der Natur. Sie findet sich in Schneckengehäusen und Muschelschalen, in den Blattstellungen unzähliger Pflanzen, bei den vor Jahrmillionen ausgestorbenen Ammoniten und bei ihrem zeitgenössischen Nachfahren, dem Nautilus oder Perlboot.
Die Augen im Pfauenschweif liegen ebenso auf den Ästen logarithmischer Spiralen, wie die einzelnen Blüten der Margerite, die Kerne einer Sonnenblume und die Samenschuppen eines Kiefernzapfens.
Und sogar die Anzahl dieser Spiraläste entspricht den Zahlen der Fibonacci-Reihe: 13, 21, 34, 55, 89 undsoweiter. “Man hat sogar”, schreibt György Doczi in seinem Buch Die Kraft der Grenzen,” Sonnenblumen mit 89 und 144 oder mit 144 und 233 entgegengesetzten Spiralen gefunden.” Und er fügt hinzu: “Auch wir, die wir uns nicht mehr vor rachsüchtigen Göttern fürchten, empfinden Ehrfurcht und Staunen angesichts dieser unerwarteten Präzision eines Wachstumsmusters der Natur”.
Das Grundmuster einer logarithmischen Spirale lässt sich sehr einfach mit Hilfe der Fibonacci-Reihe konstruieren: man fügt einfach Viertelkreise aneinander, deren Radius den Fibonacci-Zahlen entspricht. 1, 1, 2, 3, 5, 8, 13, 21 undsoweiter. Erfahrungsgemäß ist man, wenn man in Zentimetern rechnet, beim 8. oder 9. Kreisviertel am Rande des Blattes angekommen. Aber es ist ein aufregender Gedanke, dass man, zumindest theoretisch, diesen Prozess unendlich lange fortsetzen könnte.
Die logarithmische Spirale endet nie, sie führt uns buchstäblich, auch wenn wir dieses Ziel nie erreichen können, in die Unendlichkeit.
Spiegelungen - Reflections of Nature
Neben den bereits erwähnten radialen Symmetrien, wo mehrere Symmetrieachsen vom Mittelpunkt nach außen streben, finden wir in der Natur die bilaterale Symmetrie mit nur einer Symmetrieachse. Sie wird u.a. von den Wirbeltieren bevorzugt und von den jüngsten Kindern der Pflanzenfamilie - den Orchideen.
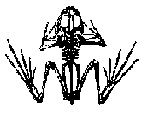Es erscheint dies als ein genialer Kunstgriff der Natur, um mit einfachsten Mitteln eine Fülle verschiedener Formen zu erzeugen: lege eine Mittelachse fest, und spiegle daran die gesamte Struktur. Als Beispiel hier das Skelett eines Frosches.
Man kann dieses Verfahren nachvollziehen, indem man zum Beispiel eine beliebige Bildstruktur (Blüten, Blätter, vertrocknetes Laub, Baumrinde,
Gesteinsformationen, undsoweiter) an einer Mittelachse spiegelt.
Es kommen dann ganz neue Formen zum Vorschein, seltsame Gestalten, Gesichter, insektenhafte Gebilde, Gnome und Dämonen und außerirdische Wesen. Und man entdeckt immer mehr davon, je länger man die Bilder betrachtet.
Jedes “Gesicht” ist eine an einer Mittelachse gespiegelte Struktur. Dies weiß unser optisches Gedächtnis aus Erfahrung. Vielleicht neigen wir deshalb dazu, in allem, was an einer Mittelachse gespiegelt ist, ein Gesicht zu sehen.
Die hier gezeigten Beispiele stammen von einer Felsformation, gefrorenen Blättern in einer Pfütze, einem vereisten Tujazweig, einer Succiniblüte, einem alten Stück Holz und der Rinde eines alten Baumes.
Wird das gespiegelte Bild ein weiteres Mal gespiegelt, so tauchen wieder radiale Symmetrien auf, und es entstehen Formen, die an Mandalas erinnern.
Hier waren es herbstliche Blätter von wildem Wein und gefrorene Kastanienblätter, die einmal vertikal und dann nocheinmal horizontal gespiegelt wurden.
Artikel zu dem Fernsehfilm
“Dr. Jennys Klangfiguren, oder: die formbildende Kraft der Schwingung”
Ende des 18. Jahrhunderts entdeckte der deutsche Physiker Ernst Chladni, dass sich auf einer Platte aus Holz, Glas oder Metall, die man mit Sand oder feinem Pulver bestreut und dergestalt an einem Punkte festgeschraubt hat, dass sie frei schwingen kann, hübsche und regelmäßige Muster bilden, wenn man mit einem Geigenbogen daran entlang streicht.
Die “chladnischen Klangfiguren” erregten seinerzeit in der wissenschaftlichen Welt einiges Aufsehen - aber da sich mit der vergleichsweise primitiven “Geigenbogenmethode” nur eine begrenzte Zahl von Mustern erzeugen ließ, erschöpfte sich das Interesse nach und nach.
Chladnis Experimente fristeten ein wenig beachtetes Dasein in den Physikbücher, bis - Ende der 50er Jahre - der Schweizer Arzt, Maler und Forscher Dr. Hans Jenny sich ihrer annahm und sie weiterentwickelte. Er prägte für seine Experimente den Ausdruck “Kymatik” - abgeleitet von dem griechischen Wort “kyma”: Welle oder Schwingung.
Dr. Jenny erkannte rasch, dass Chladnis einfache “Geigenbogenmethode” keine nach den Maßstäben moderner Naturwissenschaft akzeptablen und reproduzierbaren Ergebnisse liefern konnte, und entwickelte neue und bessere Methoden.
Die am häufigsten verwendete bestand darin, Metallplatten durch piezo-elektrische Kristalle in Schwingung zu versetzen.
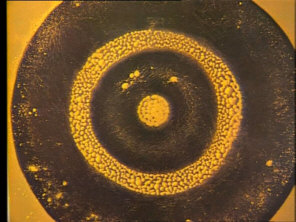
Solche Kristalle, die unter anderem auch in Quarzuhren verwendet werden, beginnen zu schwingen, wenn man sie unter Strom setzt.
Mit Hilfe eines Generators lassen sich dabei Frequenz und Stärke der Schwingung exakt steuern.
Außerdem benutzte Hans Jenny verschiedene Membranen, die direkt oder indirekt durch Lautsprecher angeregt wurden. Auf diese Weise konnte er auch die Schwingung der menschlichen Stimme in Klangfiguren umsetzen.
Hans Jenny verwendete eine Fülle verschiedener Substanzen für seine Experimente: Quarzsand und Lycopodium, Flüssigkeiten (wie z.B. Alkohol, Wasser, Glyzerin, Parafinöl oder Eiklar), ferner pastose, breiartige Gemenge aus Gips oder Kaolinerde, und Eisenstaub, der in einem Magnetfeld in Schwingung versetzt wurde und dabei wandernde und in den Raum hinausgreifende Gebilde formte.
Dokumentiert wurden diese Experimente durch eine Fülle von Fotografien und Filmaufnahmen - zum Teil mit Hochgeschwindigkeitskameras die bis zu 10000 Bilder pro Sekunde belichten konnten.
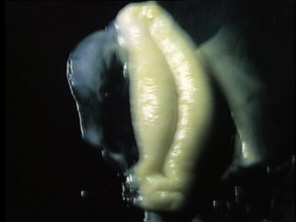Neben dem ästhetischen Reiz ihrer Muster ist noch etwas anderes an den Klangfiguren, die Hans Jenny erzeugte, bemerkenswert: ihre Ähnlichkeit nämlich mit Formen und Strukturen, die sich in der Natur finden und mit uralten Symbolen der Menschheit.
Schwingendes Glyzerin erzeugt Muster, die an Wirbeltierskelette erinnern.
Breiartige Gemenge bilden formen, die Muschelschalen oder Schneckengehäusen ähneln.
Mit einer zähen Flüssigkeit vermischtes Eisenmehl formt sich, in einem Magnetfeld schwingend, zu räumlichen Gebilden mit pflanzenhaften Strukturen.
In einem schwingenden Wassertropfen bilden sich harmonische Muster mit polygonaler Symmetrie - Zweieck, Dreieck, Viereck, Fünfeck, Sechseck, Achteck, Zehneck und Zwölfeck - die sich in ungeheurer Vielfalt bei Pflanzen und Tieren wiederfinden.
Bei einer bestimmten Frequenz bildet der Wassertropfen beispielsweise ein Pentagramm - wie es sich im Bauplan unzähliger Blumen zeigt, oder in einem quergeteilten Apfel (siehe oben), oder in den Skeletten von Meerestieren, von Seesternen, oder Radiolarien. Diese winzigen Einzeller verwirklichen in ihren Siliziumskeletten aber auch Vierck-, Sechseck- und Zwölfecksymmetrien, die sich allesamt bei entsprechender Frequenz auch im Wassertropfen bilden.
Die Frage, wie Gestaltbildung und Gestaltwandlung bei Lebewesen zu Stande kommt, ist in der Naturwissenschaft derzeit noch ungeklärt. Die alten “Regulatormolekül-Modelle” von Monod und Jacob aus den 50er Jahren werden heute von zahlreichen - vor allem jüngeren - Wissenschaftlern nicht mehr akzeptiert. Man bietet statt dessen Konzepte an, die mit dem Begriff des “morphogenetischen”, des “formbildenden Feldes” arbeiten. Darunter ist eine Art transzendentes Ordnungsfeld zu verstehen, das die Materie in der Bewegung ordnet.
Jenny’s Klangfiguren zeigen gewissermaßen “morphogenetische Felder” in Aktion. Und sie zeigen auch, was mit Hilfe solcher Felder an Gestaltbildung geleistet werden kann.
Diese “Schwingungsfelder” sind selbst nicht materiell, aber sie ordnen Materie in der Bewegung zu stabilen Mustern und Formen. Die einzelnen Bestandteile wechseln und wandern, das Muster bleibt dabei jedoch konstant. Ähnliches ist auch bei Lebewesen zu beobachten, die ihre materiellen Bestandteile im sogenannten Stoffwechsel ständig austauschen und erneuern, ihre Gestalt dabei aber erhalten.
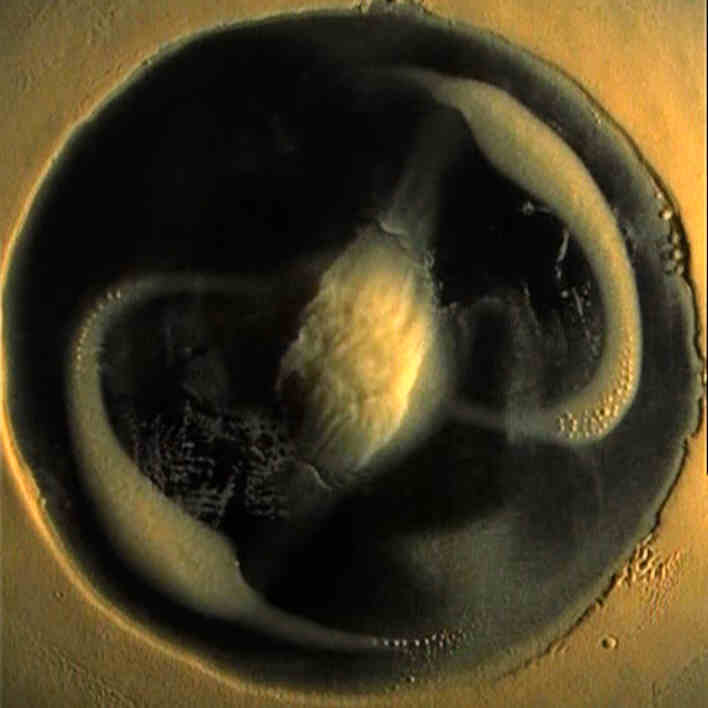Verschiedene Klangfiguren zeigen auch eine verblüffende Ähnlichkeit mit geographischen Strukturen der Erdoberfläche oder mit kosmischen Gebilden, wie z.B. galaktischen Spiralnebeln.
Welche Konsequenzen könnten sich aus solchen Analogien für unsere wissenschaftlichen Weltbilder ergeben?
Im Johannesevangelium heißt es: “Am Anfang war das Wort”. Und Wort ist Klang, ist geordnete Schwingung. Könnte man den Kosmos also als eine Art Klangfigur betrachten? Statt “Urknall” also “Urklang”? Ein sicherlich tröstlicher Gedanke. Aber bloße Ähnlichkeit ist noch kein Beweis. Und derzeit beantworten Dr. Jennys Experimente mit Klangfiguren noch keine Fragen, sie werfen vielmehr welche auf. Wenn man allerdings Antworten fände auf diese Fragen, dann könnte damit ein erheblicher Wandel unserer heutigen Denkmodelle verbunden sein.
P.S.: Ein kongenialer Nachfolger von Hans Jenny ist Alexander Lauterwasser. Seine Klangfigurenexperimente finden sich in dem Buch "Wasser Klang Bilder", AT-Verlag (ISBN 3-85502-775-7).
Zurück zum Anfang
Zurück zu "Jurassic Park"
Zurück zu "Filme & Hörspiele"